树状数组

Binary Index Tree

1.树状数组概述

• 产生需求：当我们多次求解一个数组的任意区间和时，如果数组的元素发生了改变，那我们所有的结果都要重新计算，这样的代价非常大
• 优化之处：树状数组则通过另外建立一个管理数组用来分级管理我们原来的数组。在管理数组中的每个元素都只管理部分的数据，所有当我们再次面临数据更改的问题时，我们就只需更改部分管理数组元素即可
  

---

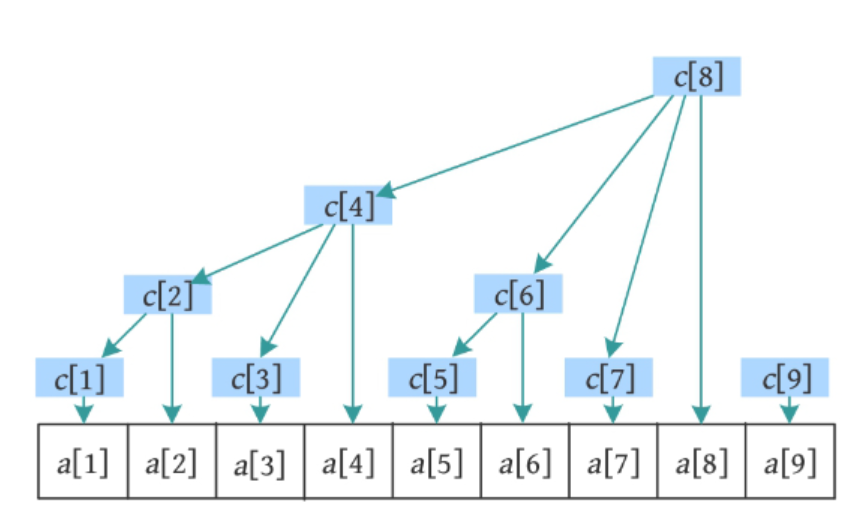
2.一维树状数组

管理数组c[]长度分配

• 引入lowbit(x)函数：x&（-x_补码）
• c[i]包含的数据个数 = lowbit(i)

  前驱和后继

• c[i]的直接前驱：c[i]左侧紧邻的子树的根→c[i-lowbit(i)]
• c[i]的直接后驱：c[i]的父节点→c[i+lowbit(i)]
• c[i]的前驱：c[i]的直接前驱、直接前驱的直接前驱……→c[i]左侧所有子树的根
• c[i]的后继：c[i]的直接后继、直接后继的直接后继……→c[i]的所有祖先

  前缀和查询算法

  int sum(int i){
    int sum=0;
    while(i>0){
        sum+=c[i];
        i-=lowbit(i);
    }
    return sum;
  }
  

  点更新算法

• 若a[i]+=delta,则只需把c[i]及其祖先节点都加上delta即可

  void add(int i,int delta){
    while(i<=n){
        c[i]+=delta;
        i+=lowbit(i);
    }
  }
  

  树状数组的下标需要从1开始，因为lowbit(0)会陷入死循环

  区间和查询算法

  int sum_plus(int i,int j){
    return sum(j)-sum(i-1);
  }
  

  建立树状数组

  for(i=0;i<n;i++){
    add(i+1,a[i]);
  }
  

  把建立的过程看成是n次点更新即可

---

3.二维树状数组

查询前缀和

• 实际上是求矩阵(1,1)到(x,y)的区间和

  int sum(int x,int y){
    int sum=0;
    for(i=x;i>=1;i-=lowbit(i)){
        for(j=y;j>=1;j-=lowbit(j)){
            sum+=c[i][j];
        }
    }
    return sum;
  }
  

  点更新

• 若a[x][y]+=delta,则其所有的父节点都加上delta

  void add(int x,int y,int delta){
    for(i=x;i<=n;i+=lowbit(i)){
        for(j=y;j<=n;j+=lowbit(j)){
            c[i][j]+=delta;
        }
    }
  }
  

  查询区间和

  

  int sum_plus(int x1,int y1,int x2,int y2){
    return sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1)
  }
  

  建立树状数组

• 同上